About

Large Language Models:

The capabilities of Large Language Models (LLM’s) to process data from different modalities and excel at different tasks ranging from information extraction, question and answering, math, coding, and recently reasoning simply shows the potential of this technology. Intuitively the complexities of training these models on different datasets/data mixes, opting different architectural choices, choosing different alignment strategies [1] seemingly could suggest picking a specific model for each task, but LLM’s are geared towards being considered as general task solvers.

image

Dataset

Customized MLRC Data built from [2].

image

Study-1:

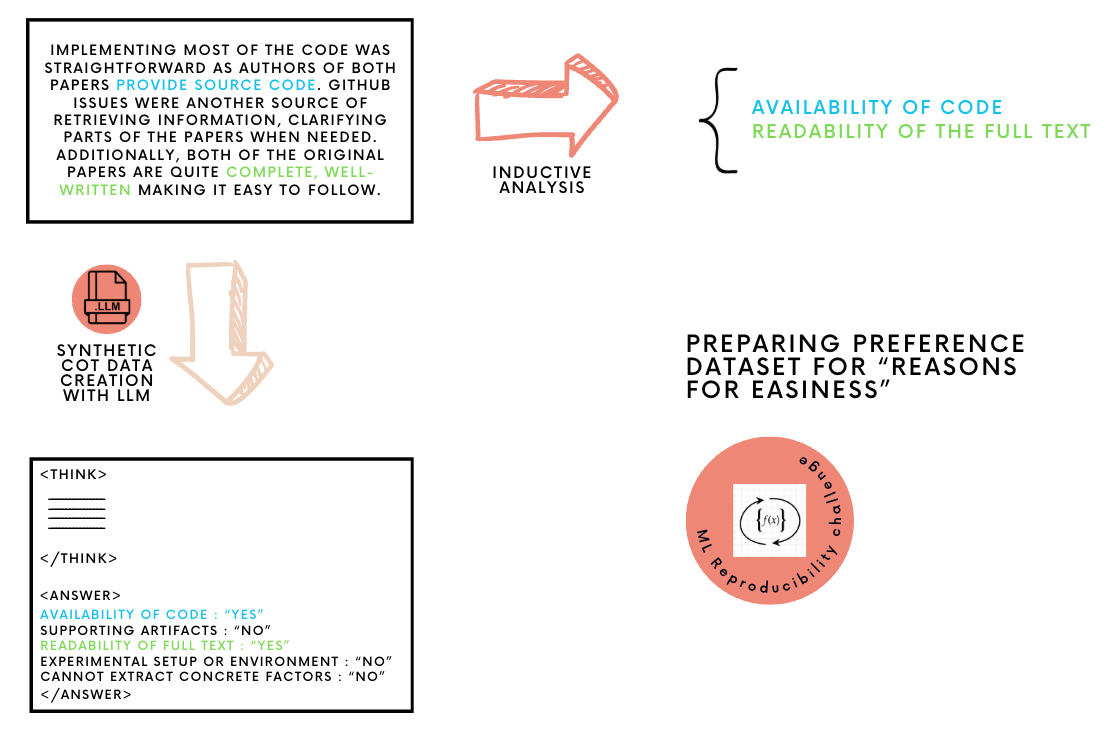
For this study we are going to test out three use-cases, Labelling, Information Extraction, and LLM as a Judge. We are going to use the dataset from the paper Laying Foundations to Quantify the “Effort of Reproducibility” [2]. The dataset and the tasks outline a good experimentation framework to effectively utilize Large language models for computational social science tasks [3].

In-context-learning notebook:

Open In Colab

Study-2:

For this study we are going to use the Reproducibility dataset from the paper Laying Foundations to Quantify the “Effort of Reproducibility” [2] to preference tune answers using the Direct Preference Optimization(DPO) algorithm. DPO unlike other reinforcement algorithms directly applies maximum likelihood on the preference dataset to perform implicit reward modeling. Ideally, similar to most RL algorithms we would be applying the same reward maximization via KL divergence constraint. Theoretically, DPO is RL free, and doing a simple classification on a given a dataset $D$ that includes chosen and rejected responses. Learn more about DPO from the original paper [4].

$$ L_{DPO}(\pi_{LLMSciSci}: \pi_{LLM-instruct}) ;=; - ,\mathbb{E}{\bigl(x,,r^+,,r^-\bigr) \sim D_{ReproEffortDataset}} \Bigl[ \log ,\sigma!\Bigl( r_\theta(x,r^+) ;-; r_\theta(x,r^-) \Bigr) \Bigr] $$

$$ r_\theta(x, r) ;=; \beta ,\log \frac{\pi_{LLMSciSci}(r ,\vert, x)}{\pi_{LLM-instruct}(r ,\vert, x)} $$

where the $r_{\theta}$ is computed

  • using $r^+$(human preferred response), and $r^-$(rejected responses).
  • for the models $\pi_{LLMSciSci}$ and $\pi_{LLM-instruct}$.
  • $r_{\theta}$ captures the log-probability of the chosen vs rejected responses on $D_{ReproEffortDataset}$.
  • $\pi_{LLM-instruct}$ is the instruct-tuned open weight reference model.
  • $\pi_{LLMSciSci}$ is the final RL model intended to be preference-tuned on $D_{ReproEffortDataset}$.

DPO Notebook:

Open In Colab

Study-3:

For this study we are going to use the Reproducibility dataset from the paper Laying Foundations to Quantify the “Effort of Reproducibility” [2] to optimize policy gradients using Group Relative Policy Optimization(GRPO) algorithm. GRPO is an online learning algorithm where the model uses generated completions to learn how to maximize advantages and get better at generating completions at every given step. Learn more about the GRPO from the original paper [5].

Format rewards

$$ R_{\text{format}}(c) = \begin{cases} 1.0 & \text{if } c \text{ matches pattern } \texttt{… } \ 0.0 & \text{otherwise} \end{cases} $$

Label rewards

$$ R_{\text{label}}(c) = \begin{cases} 0.5 & \text{if } c \text{ matches format AND } \text{extracttext}(c, \text{“label”}) \text{ is valid onehot} \ 0.0 & \text{otherwise} \end{cases} $$

Stepwise rewards

$$ R_{\text{stepwise}}(c) = r_1 + r_2 + r_3 + r_4 $$

$$ r_1 = \begin{cases} 0.125 & \text{if there exists non-empty text within } \texttt{} \ 0.0 & \text{otherwise} \end{cases} $$

$$ r_2 = \begin{cases} 0.125 & \text{if text consists only of 0’s and 1’s (ignoring brackets, commas, whitespace)} \ 0.0 & \text{otherwise} \end{cases} $$

$$ r_3 = \begin{cases} 0.125 & \text{if text starts with ‘[’ and ends with ‘]’} \ 0.0 & \text{otherwise} \end{cases} $$

$$ r_4 = \begin{cases} 0.625 & \text{if text passes the } \textit{isvalidonehot()} \text{check} \ 0.0 & \text{otherwise} \end{cases} $$

Hamming loss correctness reward

$$ R_{\text{hamming}}(p, c, \text{doi}, \text{ltype}) = \begin{cases} 1 - HL(y_{\text{true}}, y_{\text{pred}}) & \text{if } \text{extracttext}(c, \text{“label”}) \text{ is valid onehot} \ 0.0 & \text{otherwise} \end{cases} $$

Conditional Reasoning trace length award

$$ R_{\text{condcotsteplabel}}(c) = \begin{cases} R_{\text{stepwise}}(c) + \alpha \cdot R_{\text{cotlength}}(c) & \text{if } R_{\text{stepwise}}(c) \geq \tau \ R_{\text{stepwise}}(c) & \text{otherwise} \end{cases} $$

GRPO Notebook:

Open In Colab

References(s):

  1. A Survey of Large Language Models
  2. Laying Foundations to Quantify the “Effort of Reproducibility”
  3. Can Large Language Models Transform Computational Social Science?
  4. Direct Preference Optimization: Your Language Model is Secretly a Reward Model
  5. DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models

Authors and Contributors:

Akhil Pandey, Want to contribute see your name here :), Open an Issue ?

Acknowledgement

The computing resources for this work is supported in part by the Google Cloud Research Credits Grant 331845891, and Lambda Labs Credits through the support program D1: CSC-SUPPORT-CDFF-2025-3-31.

Lambda logo GCP